堆排序可以分成两步，一：将给定的数组建立成堆。 二：不断的移除根节点，然后重组堆。并移除的根节点插入到数组中。

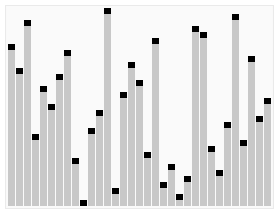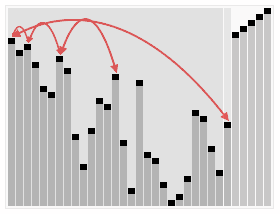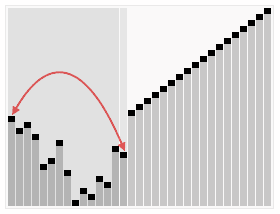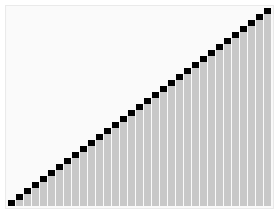
image
图片来源：维基百科

堆的定义

关于堆的定义，可以查看数据结构之堆

特点

  • 堆排序是一种不稳定的排序。
  • 堆排序的时间复杂度为 O(nlogn)。
  • 堆排序的空间复杂度为 O(1)。

堆排序的伪代码：

ALGORITHM heapSort(A) is
  buildHeap(A, length(A) - 1)
  FOR i ← length(A) - 1 downto 1
    swap A[0] and A[i]
    heapify(A, 0, i-1)
  END FOR
END ALGORITHM

建立最大堆的伪代码：

ALGORITHM buildHeap(A, hi) IS
  FOR i ← hi/2 - 1 downto 0
    heapify(A, i, hi)
  END FOR
END ALGORITHM

最大堆调整heapify的伪代码：

// 递归法
ALGORITHM heapify(A, lo, hi) is
  maxIndex ← lo
  l ← 2 * lo + 1
  r ← 2 * lo + 2

  IF l <= hi and A[l] > A[maxIndex]
    maxIndex ← l
  END IF

  IF r <= hi and A[r] > A[maxIndex]
    maxIndex ← r
  END IF

  IF maxIndex != lo
    swap A[lo] and A[maxIndex]
    heapify(A, maxIndex, hi)
  END IF
END ALGORITHM

// 循环迭代法
ALGORITHM heapify(A, lo, hi) IS
  temp ← A[lo]
  j ← 2 * lo + 1
  WHILE j <= hi
    IF j < hi and A[j] < A[j+1]
      j ← j + 1
    END IF
    IF temp >= A[j] 
      break
    END IF
    A[lo] = A[j]
    lo ← j
    j ← 2 * j + 1
  END WHILE
  A[lo] ← temp
END ALGORITHM